physics on a flat earth

Summary
We claim it is possible to create a representation of reality where the earth is represented by a disc. The method by which this model is created can be generalized to any shape, even a globe.
To derive the model, we start 2000 years ago by generalizing Eratosthenes. Pythagoras was the first to consider a spherical earth, mostly on aesthetic grounds. Eratosthenes was the first to test this theory. He assumed a spherical earth and straight light and saw his assumptions matched his measurements. However what Eratosthenes really measured was the relationship between earth-shape and lightray-shape. He did not measure earth curvature.
Undoing this assumption we can instead assume a flat earth and from the measurements it would follow that light needs to curve. The curvature of lightrays can be measured by for example measuring the amount of missing hull on a ship leaving the harbor. This will give us an equation and from this equation we can rederive 2000 years of physics and create a consistent set of formulas.
In physics, once you have 2 models one generally devises a test to prove which model is correct, or one tries to prove both models are equal. In this instance it can be shown the flat earth model is equivalent to the globe model. This can be done by a coordinate transformation.
The rest of this paper will first explore the coordinate transformation. Intuitively it can be seen that
- lat/lon coordinates are invariant between flat earth and globe earth.
- All formulas that work on lat/lon coordinates will work on both models. Haversine for example will produce correct distances on a flat earth model.
- There exists a transformation from cartesian to lat/lon coordinates and so all physics formulas can be converted into shape-agnostic ones.
- Extending this to 3 dimension (lat, lon, distance), will complete this work.
Azimuthal coordinate transformation onto a cylinder
Intuition: Fill space with concentric sphere’s around the origin. For every sphere , transform it into a disc with an an azimuthal equidistant projection and finally insert the disc into a cylinder at a height equal to the radius of the sphere.
Azimuthal transformation is a coordinate transformation that converts cartesian space into a cylinder. The transformation is lossless and reversible (ie it’s a transformation, not a projection). Within the resulting cylinder, any shell around the origin will become a flat disc (an azimuthal projection of that sphere).
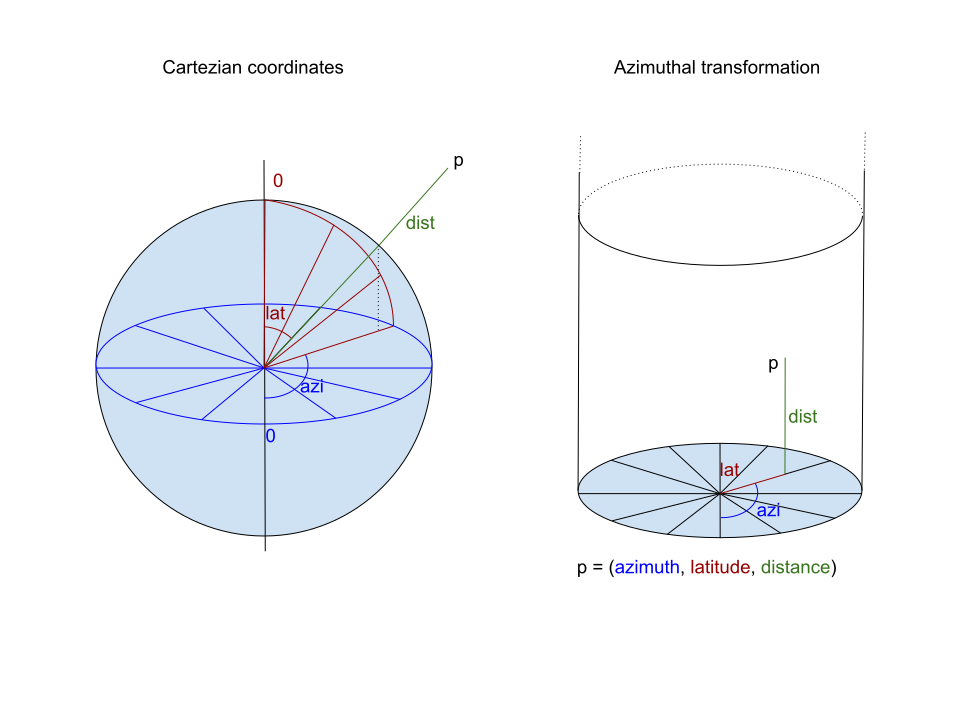
Definition: any point in cartesian space (x, y, z) can be represented with celestial coordinates (azimuth, altitude, distance) relative to an origin. All points on a sphere around this origin with radius d will have the same distance in celestial coordinates, ie all their coordinates will look like (azimuth, altitude, d). Ie a flat 2D structure at height d. (azimuth, altitude) can be drawn like a AE projection map: azimuth as an angle around the center, altitude as a distance from said center. And by doing so, 3D space will be transformed into an infinitely high cylinder.
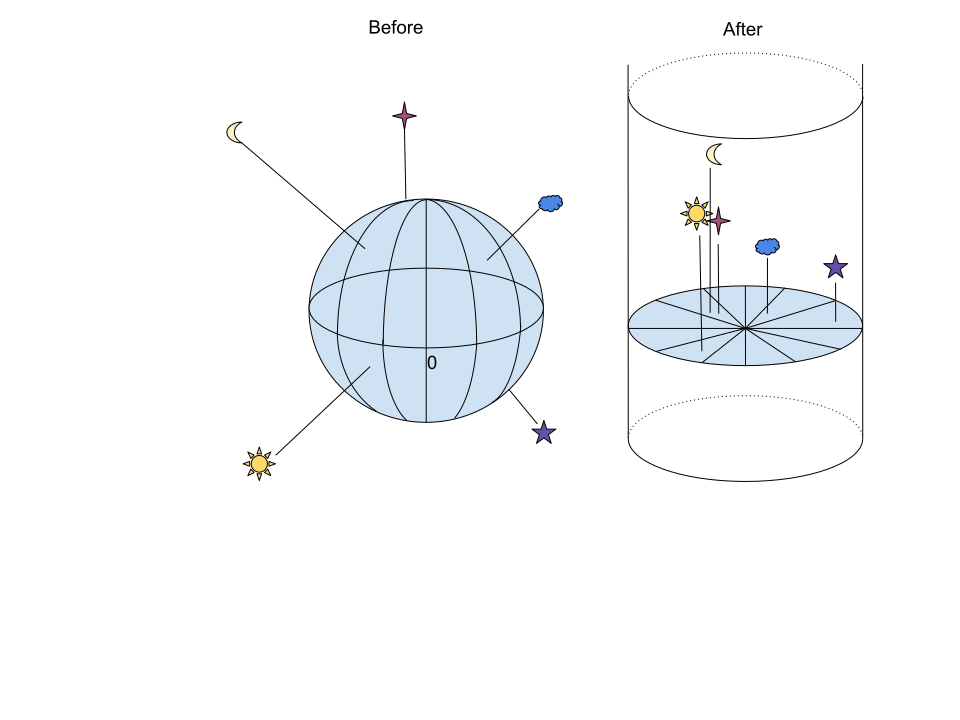
Azimuthal transformation with the earth as origin
When performing an azimuthal transformation with the center of the earth as origin, it will transform all of space into an infinitely high cylinder. In this cylinder, at height 0 will be the center of the earth. Around 6371km will be an azimuthal projection of earth (a flat earth). Above the disc earth, will be all celestial objects at their cartesian distance from the center of the earth.
Physics in the azimuthal cylinder
Azimuthal transformation is lossless and reversible. It is a coordinate transformation not a projection: it’s just like polar coordinates and cartesian ones: they represent the same thing in a different way and you can easily switch back and forth between them.
Physics in this cylinder work exactly the same and equally expressive as in the cartesian plane. Anything that can be proven in cartesian space, can also be proven in an azimuthal transformed cylinder by at most 2 extra coordinate transformations
Proof_in_azimuthal(claim) = convert_to_azimuthal(prove_in_cartesian(convert_to_cartestian(claim)))
Here are some examples of various coordinate transformations demonstrating day/night and seasons. Note that the transformation turns straight lines into curves, and so light travels in curves on a flat earth. This is why the sun doesn’t illuminate the entire disc. Also note that coordinate transformations can be applied one after the other to further transform the world.




So what shape does the earth have
In this paper we do not make any claims about the shape of the earth in reality. All we prove is that physics can be made to work in a model that looks like a flat earth.
Is this useful
- Scientifically speaking: Probably not. Physics has understood coordinate transformations for a long time and they’re generally used when it makes the math easier. In this case it’s very unlikely it will lead to easier math (though we have found some specific operations which are easier on a cylindrical universe). One potential use we could imagine for this model is visualization. The dimensions of space are so unfathomably large that in some cases it might be fun to have a tangible cylinder to observe.
- Philosophically speaking deciding between models would be a candidate for Occams razor and we doubt this paper would provide any new insights. Everything was probably already long said during heliocentric versus geocentric debates.
- Theologically speaking: Even though one model is shaped like a snowglobe, it will probably not perform as expected. For observers within the universe, space is still infinite and sun and stars are still unfathomably far away. Only for an observer outside the universe would it look like an actual snowglobe.
The most likely result this paper will bring forth, will be the loss of a week of the life of its author 🙂
What happens when you walk of the edge
The edge is a mathematical artifact. Altitude is only defined between [0, π] and when we transform with any other point than the northpole as the center of our map, the southpole circle suddenly becomes continuous.
However if you must have an answer: you teleport to the other side of the map.
Properties of the transformation
Azimuthal transformation preserves some properties but breaks several others:
- Coordinates in azimuthal space are numerically identical to celestial coordinates. Latitude and longitude on the disc are still the same after transformation
- Spheres and shells about the origin become circles and discs
- azimuth and distance are preserved, altitude is “broken”
- Angles and distances involving altitude need special formulas
Optics in a flat universe
3D optics:
Drawing this horizon onto an azimuthal cylinder, it will produce a cone and as noone can see below the horizon, the space outside of the cone is not visible. No rays of light emitted from the center of the cone, will ever be able to escape it. (note that this cone should be aptly distorted when moving to other positions than the northpole.)
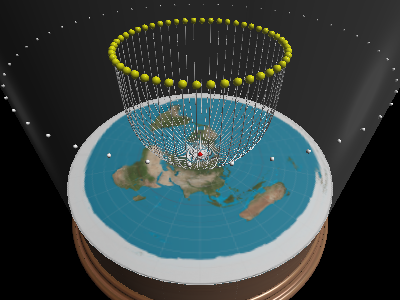
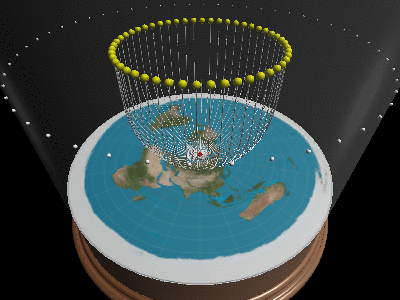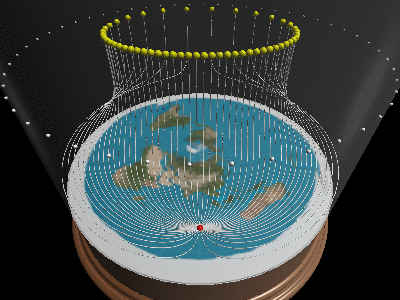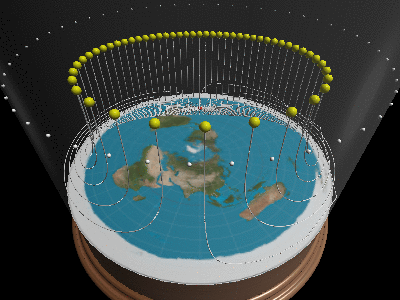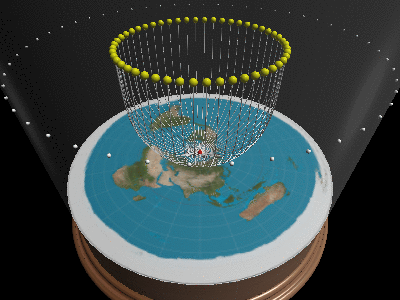
Can you explain day/night/seasons/eclipses/…?
Once we realize travels in curves, and that one cannot see below/outside the horizon, all of optics suddenly makes sense. When the sun moves inside the horizon-cone it will be day, when it moves outside, it’s night. By having the sun change altitude, it will change positions and explain why there are longer days in summer than winter.

Finally the phases of the moon can also be explained. The light rays from the sun to the moon also travel in curves. If the earth gets in the way of such a curve, the light will never reach the moon and the moon will be dark. The flat earth Society has a pretty good write-up about light bending physics. And even though we do not agree with the cause of light bending, the drawings and explanation are pretty good.
Why does the earth look like a globe from space?
Light curves. If you look at a flat line/plane in the distance, the light reflected by nearby points will curve less than light from faraway points. Meaning that light from faraway points reaches our eye at a lower angle, making the image look like a globe. You might call it flat earth perspective 🙂
How to see flat earth
It works for us by looking at one of them ships with a missing body. What I SEE is a ship obstructed by the water at the horizon.
In globe theory this is EXPLAINED by the curvature of the earth.
In the flat model, this is EXPLAINED by the curvature of light. Just try to superimpose the upwards bending lightrays from the model on the picture.
Are you a flat earther
No, just tired of the debate 🙂