The shape of light
The shape of the earth and the shape of a light ray are not the same. Therefore in a flat earth model, light should be modeled as a curve.
Experiment:
A shark with a laser sits on the surface of the water. A physicist jumps in a boat and sails away from the shark. At regular intervals she measures the height of the laser dot on the sail. We place the measurements on a graph and find:
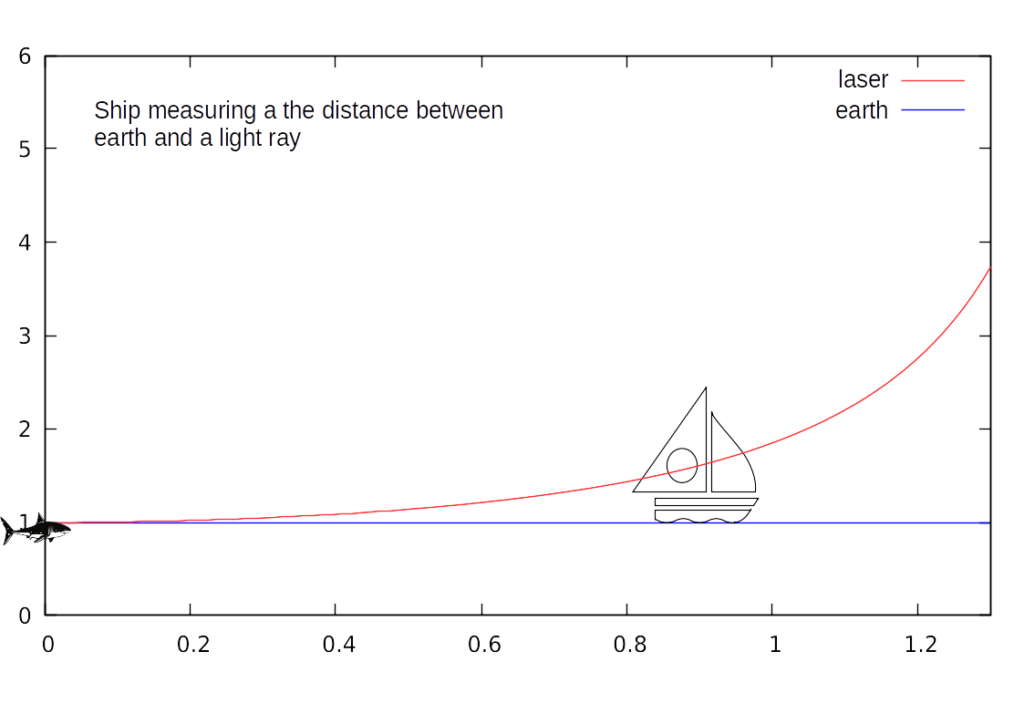
Doing a best fit on the data we find that the equation y = sec(x) is a very good fit for this curve.
Horizon distance
The physicist in the boat climbs into the mast until the laser dot is at eye-height. She will see the shark at the horizon. If she climbs higher, the shark will be in front of the horizon. If she goes below the laser dot, the shark is behind the horizon and can’t be seen.
Example:
Given a physicist at height h, the lightray equation tells us, h = sec(d) – 1. The graph uses Flat Earth Miles (FEM) on its axis. 2π FEM correspond with 40,030km: the diameter of the disc. Let’s say the physicist is at a height of 10m (1.570e-6 FEM). Then the light equation tells us we should see the horizon d at a distance of 11.288km (1.77e-3 FEM). This is exactly the same distance a good horizon distance calculator will give.
Objects obscured by curving light
Ignoring the shark, our captain sees a lighthouse in the distance. Because of bending light the bottom of the lighthouse is obscured. Remember that we can’t see below the horizon. Anything below it is obscured by the earth.
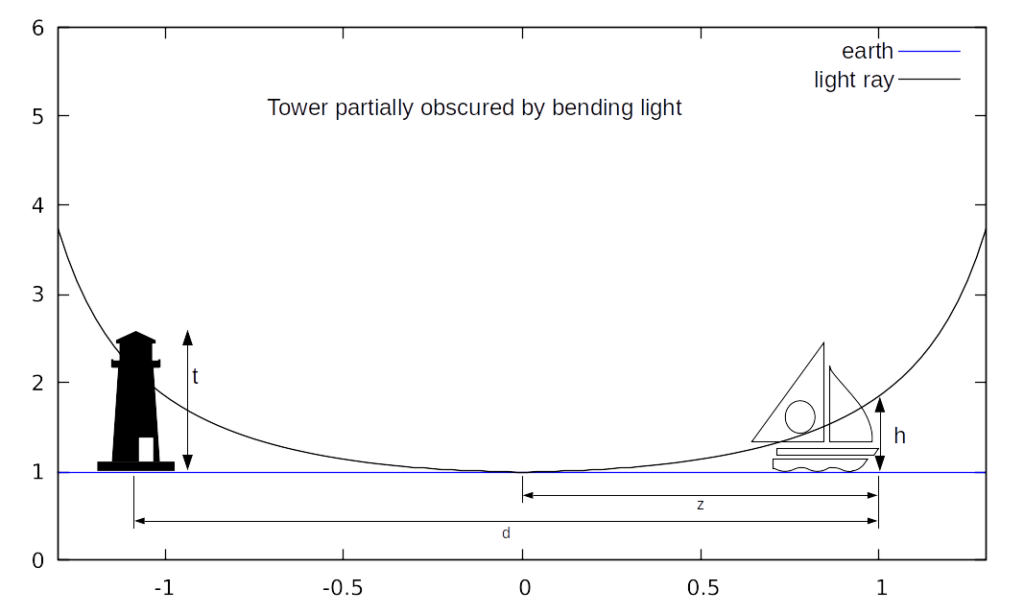
Example:
The captain stands at a height of 7m (1.099e-6 FEM). And we know the lighthouse is at a distance d of 20km (3.139e-3 FEM). Then we know that the horizon is at a distance z = 1.482e-3 FEM (previous paragraph). The distance from the lighthouse to the horizon is d-z. The curve to the lighthouse is still y = sec(x), so the obscured height is given by t = sec(d-z) – 1 = 1.373e-6 FEM (8.745m). Exactly what the globe model would predict.